Linear Structure

1. Introduction

2. Stacks

3. Queues

4. Deques

3.1~3.2 What Are Linear ADT?

They are data collections whose items are ordered depending on how they are added or removed. Once an item is added, it stays in that position relative to the other elements that came before and came after it. Collections such as these are often referred to as linear ADT.

Linear ADT can be thought of as having two ends. Sometimes these ends are referred to as the left and the right, or in some cases the front and the rear.

What distinguishes one linear structure from another is the way in which items are added and removed, in particular the location where these additions and removals occur.

3.3 Stacks

A stack (sometimes called a push-down stack) is an ordered collection of items where the addition of new items and the removal of existing items always takes place at the same end. This end is commonly referred to as the top. The end opposite the top is known as the base.

The base of the stack is significant since items stored in the stack that are closer to the base represent those that have been in the stack the longest. The most recently added item is the one that is in position to be removed first. This ordering principle is sometimes called LIFO, or last in, first out.

Almost any cafeteria has a stack of trays or plates where you take the one at the top, uncovering a new tray or plate for the next customer in line. Imagine a stack of books on a desk. The only book whose cover is visible is the one on top. To access others in the stack, we need to remove the ones that are sitting on top of them.

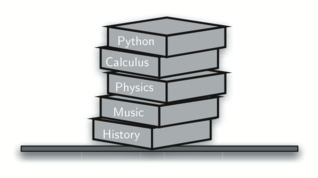
Assume you start out with a clean desktop. Now place books one at a time on top of each other. You are constructing a stack. Consider what happens when you begin removing books. The order that they are removed is exactly the reverse of the order that they were placed.

Stacks are fundamentally important, as they can be used to reverse the order of items. The order of insertion is the reverse of the order of removal:

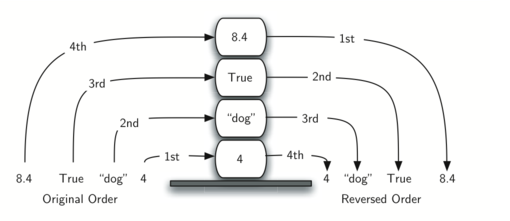
For example, every web browser has a Back button. As you navigate from web page to web page, those pages are placed on a stack (actually it is the URLs that are going on the stack). The current page that you are viewing is on the top and the first page you looked at is at the base. If you click on the Back button, you begin to move in reverse order through the pages!

3.4 The Stack Abstract Data Type

The stack operations are given below:

• Stack() creates a new stack that is empty. It needs no parameters and returns an empty stack.

• push(item) adds a new item to the top of the stack. It needs the item and returns nothing.

• pop() removes the top item from the stack. It needs no parameters and returns the item. The stack is modified.

• peek() returns the top item from the stack but does not remove it. It needs no parameters. The stack is not modified.
• is_empty() tests to see whether the stack is empty. It needs no parameters and returns a boolean value.
• size() returns the number of items on the stack. It needs no parameters and returns an integer.

Under Stack Contents, the top item is listed at the far right:

Stack Operation	Stack Contents	Return Value
s.is_empty()	[]	True
s.push(4)	[4]
s.push('dog')	[4, 'dog']
s.peek()	[4, 'dog']	'dog'
s.push(True)	[4, 'dog', True]
s.size()	[4, 'dog', True]	3
s.is_empty()	[4, 'dog', True]	False
s.push(8.4)	[4, 'dog', True, 8.4]
s.pop()	[4, 'dog', True]	8.4
s.pop()	[4, 'dog']	True
s.size()	[4, 'dog']	2

3.5 Implementing a Stack in Python

Now that we have clearly defined the stack as an ADT, we will turn our attention to using Python to implement the stack. Recall that we will implement an abstract data type with a physical implementation called data structure.

The implementation of choice for an abstract data type such as a stack is the creation of a new class. The stack operations are implemented as methods. Further, to implement a stack, which is a collection of elements, it makes sense to utilize the power and simplicity of the list provided by Python.

Recall that the list class in Python provides an ordered collection mechanism and a set of methods. We need only to decide which end of the list will be considered the top of the stack and which will be the base. Once that decision is made, the operations can be implemented using the list methods such as append() and pop().

Assumes that the end (right) of the list will hold the top element of the stack:

class Stack:
    def __init__(self):
        self._items = []

    def is_empty(self):
        """Check if the stack is empty"""
        return self._items == []

    def push(self, item):
        """Add an item to the stack"""
        self._items.append(item)

    def pop(self):
        """Remove an item from the stack"""
        return self._items.pop()

    def peek(self):
        """Get the value of the top item in the stack"""
        return self._items[-1]

    def size(self):
        """Get the number of items in the stack"""
        return len(self._items)
  
    def __str__(self):
        return str(self._items)

import sys
sys.path.append("../pythonds3/")

#from pythonds3.basic import Stack

s = Stack()

print(s.is_empty())
s.push(4)
s.push("dog")
print(s.peek())
print(s)
s.push(True)
print(s.size())
print(s.is_empty())
s.push(8.4)
print(s)
print(s.pop())
print(s.pop())
print(s.size())

True
dog
[4, 'dog']
3
False
[4, 'dog', True, 8.4]
8.4
True
2

We could use a list where the top is at the beginning instead of at the end.

class Stack2:
    def __init__(self):
        self._items = []
        
    def is_empty(self):
        """Check if the stack is empty"""
        return self._items == []
    
    def push(self, item):
        """Add an item to the stack"""
        self._items.insert(0, item)
        
    def pop(self):
        """Remove an item from the stack"""
        return self._items.pop(0)
    
    def peek(self):
        """Get the value of the top item in the stack"""
        return self._items[0]
    
    def size(self):
        """Get the number of items in the stack"""
        return len(self._items)
    
    def __str__(self):
        return str(self._items)

In this case, the previous pop() and append() methods would no longer work and we would have to index position 0 (the first item in the list) explicitly using pop() and insert()!

s = Stack2()

print(s.is_empty())
s.push(4)
s.push("dog")
print(s.peek())
print(s)
s.push(True)
print(s.size())
print(s.is_empty())
s.push(8.4)
print(s)
print(s.pop())
print(s.pop())
print(s.size())

True
dog
['dog', 4]
3
False
[8.4, True, 'dog', 4]
8.4
True
2

This ability to change the physical implementation of an ADT while maintaining the logical characteristics is an example of abstraction at work. However, even though the stack will work either way, if we consider the performance of the two implementations, there is definitely a difference!

Recall that the append() and pop() operations were both $O(1)$. This means that the first implementation will perform push() and pop() in constant time no matter how many items are on the stack.

The performance of the second implementation suffers in that the insert(0) and pop(0) operations will both require $O(n)$ for a stack of size $n$. Clearly, even though the implementations are logically equivalent, they would have very different timings when performing benchmark testing!

Exercise: Write a function rev_string(my_str) that uses a stack to reverse the characters in a string.

#from pythonds3.basic import Stack
def rev_string(my_str):
    s = Stack()
    return r_str

rev_string("NSYSU")

3.8. Converting Decimal Numbers to Binary Numbers

Binary representation is important in computer science since all values stored within a computer exist as a string of binary digits, a string of 0s and 1s.

Integer values are common data items. They are used in computer programs and computation all the time. We learn about them in math class and of course represent them using the decimal number system, or base 10. The decimal number $233_{10}$ and its corresponding binary equivalent $11101001_{2}$ are interpreted respectively as:

$$2\times10^{2} + 3\times10^{1} + 3\times10^{0}$$

$$1\times2^{7} + 1\times2^{6} + 1\times2^{5} + 0\times2^{4} + 1\times2^{3} + 0\times2^{2} + 0\times2^{1} + 1\times2^{0}$$

But how can we easily convert integer values into binary numbers? The answer is an algorithm called Divide by 2 that uses a stack to keep track of the digits for the binary result!

The Divide by 2 algorithm assumes that we start with an integer greater than 0. A simple iteration then continually divides the decimal number by 2 and keeps track of the remainder.

The first division by 2 gives information as to whether the value is even or odd. An even value will have the digit 0 in the ones place. An odd value will have the digit 1 in the ones place. We think about building our binary number as a sequence of digits; the first remainder we compute will actually be the last digit in the sequence

We again see the reversal property that signals that a stack is likely to be the appropriate data structure for solving the problem!

The Python code below implements the Divide by 2 algorithm. The function divide_by_2() takes an argument that is a decimal number and repeatedly divides it by 2:

from pythonds3.basic import Stack

def divide_by_2(decimal_num):
    rem_stack = Stack()

    while decimal_num > 0:
        rem = decimal_num % 2
        rem_stack.push(rem)
        decimal_num = decimal_num // 2

    bin_string = ""
    while not rem_stack.is_empty():
        bin_string = bin_string + str(rem_stack.pop())

    return bin_string

print(divide_by_2(42))
print(divide_by_2(31))

101010
11111

It can easily be extended to perform the conversion for any base. In computer science it is common to use a number of different encodings. The most common of these are binary, octal (base 8), and hexadecimal (base 16).

The decimal number $233_{10}$ and its corresponding octal and hexadecimal equivalents $351_{8}$ and $E9_{16}$ are interpreted as

$$3\times8^{2} + 5\times8^{1} + 1\times8^{0}$$

$$14\times16^{1} + 9\times16^{0}$$

The function divide_by_2() can be modified to accept not only a decimal value but also a base for the intended conversion. The "Divide by 2" idea is simply replaced with a more general "Divide by base."

Base 2 through base 10 numbers need a maximum of 10 digits, so the typical digit characters 0 through 9 work fine.

The problem comes when we go beyond base 10. We can no longer simply use the remainders, as they are themselves represented as two-digit decimal numbers. Instead we need to create a set of digits that can be used to represent those remainders beyond 9

from pythonds3.basic import Stack

def base_converter(decimal_num, base):
    digits = "0123456789ABCDEF"
    rem_stack = Stack()

    while decimal_num > 0:
        rem = decimal_num % base
        rem_stack.push(rem)
        decimal_num = decimal_num // base

    new_string = ""
    while not rem_stack.is_empty():
        new_string = new_string + digits[rem_stack.pop()]

    return new_string

print(base_converter(25, 2))
print(base_converter(25, 16))

11001
19

3.9. Infix, Prefix, and Postfix Expressions

When you write an arithmetic expression such as B · C, the form of the expression provides you with information so that you can interpret it correctly.

In this case we know that the variable B is being multiplied by the variable C since the multiplication operator · appears between them in the expression. This type of notation is referred to as infix since the operator is in between the two operands that it is working on.

Consider another infix example, A + B · C. The operators + and · still appear between the operands, but there is a problem. Which operands do they work on?

Does the + work on A and B, or does the · take B and C? The expression seems ambiguous. In fact, we know something about the operators + and ·. Each operator has a precedence level. Operators of higher precedence are used before operators of lower precedence.

The only thing that can change that order is the presence of parentheses. The precedence order for arithmetic operators places multiplication and division above addition and subtraction. If two operators of equal precedence appear, then a left-to-right ordering or associativity is used.

Let’s interpret the troublesome expression A + B · C using operator precedence. B and C are multiplied first, and A is then added to that result. (A + B) · C would force the addition of A and B to be done first before the multiplication. In the expression A + B + C, by precedence (via associativity), the leftmost + would be done first.

Computers need to know exactly what operations to perform and in what order.

One way to write an expression that guarantees there will be no confusion with respect to the order of operations is to create what is called a fully parenthesized expression. This type of expression uses one pair of parentheses for each operator. The parentheses dictate the order of operations; there is no ambiguity!

The expression A + B · C + D can be rewritten as ((A + (B · C)) + D) to show that the multiplication happens first, followed by the leftmost addition. A + B + C + D can be written as (((A + B) + C) + D) since the addition operations associate from left to right.

There are two other very important expression formats that may not seem obvious to you at first. Consider the infix expression A + B. What would happen if we moved the operator before the two operands? The resulting expression would be + A B. Likewise, we could move the operator to the end, resulting in A B +. These look a bit strange.

These changes to the position of the operator with respect to the operands create two new expression formats, prefix and postfix. Prefix expression notation requires that all operators precede the two operands that they work on. Postfix, on the other hand, requires that its operators come after the corresponding operands.

A + B · C would be written as + A · B C in prefix. The multiplication operator comes immediately before the operands B and C, denoting that · has precedence over +. The addition operator then appears before the A and the result of the multiplication.

In postfix, the expression would be A B C · +. Again, the order of operations is preserved since the · appears immediately after the B and the C, denoting that · has precedence, with + coming after.

Now consider the infix expression (A + B) · C. Recall that in this case, infix requires the parentheses to force the performance of the addition before the multiplication.

However, when A + B was written in prefix, the addition operator was simply moved before the operands, + A B. The result of this operation becomes the first operand for the multiplication. The multiplication operator is moved in front of the entire expression, giving us · + A B C. Likewise, in postfix A B + forces the addition to happen first:

Infix Expression	Prefix Expression	Postfix Expression
A + B	+ A B	A B +
A + B · C	+ A · B C	A B C · +
(A + B) · C	· + A B C	A B + C ·
A + B · C + D	+ + A · B C D	A B C · + D +
(A + B) · (C + D)	· + A B + C D	A B + C D + ·
A · B + C · D	+ · A B · C D	A B · C D · +
A + B + C + D	+ + + A B C D	A B + C + D +

3.9.1 Conversion of Infix Expressions to Prefix and Postfix

The first technique that we will consider uses the notion of a fully parenthesized expression that was discussed earlier.

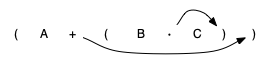
Recall that A + B · C can be written as (A + (B · C)) to show explicitly that the multiplication has precedence over the addition. Look at the right parenthesis in the subexpression (B · C) above. If we were to move the multiplication symbol to that position and remove the matching left parenthesis, giving us B C ·, we would in effect have converted the subexpression to postfix notation.

If the addition operator were also moved to its corresponding right parenthesis position and the matching left parenthesis were removed, the complete postfix expression would result:

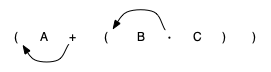
If we do the same thing but instead of moving the symbol to the position of the right, we move it to the left parenthesis, we get prefix notation. The position of the parenthesis pair is actually a clue to the final position of the enclosed operator.

So in order to convert an expression, no matter how complex, to either prefix or postfix notation, fully parenthesize the expression using the order of operations. Then move the enclosed operator to the position of either the left or the right parenthesis depending on whether you want prefix or postfix notation:

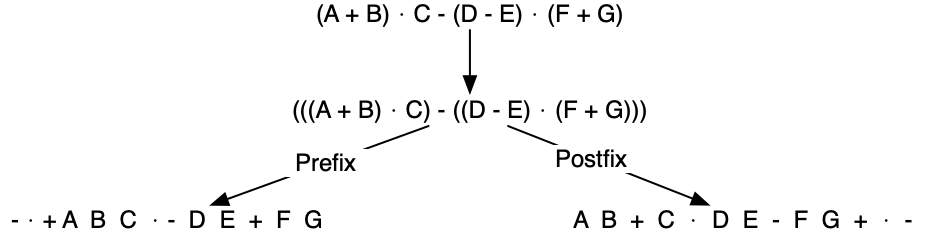
3.9.2. General Infix-to-Postfix Conversion

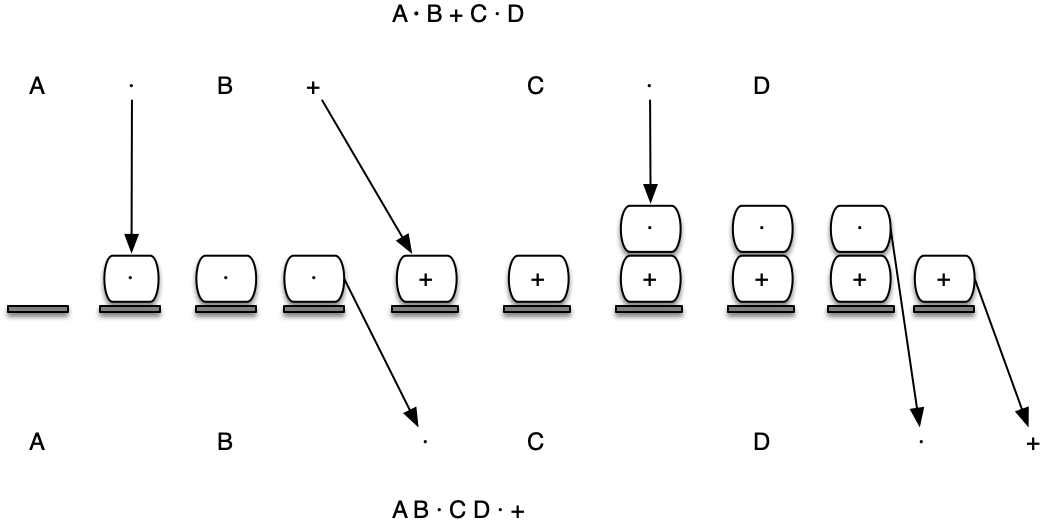
Consider once again the expression A + B · C. As shown above, A B C · + is the postfix equivalent. We have already noted that the operands A, B, and C stay in their relative positions. It is only the operators that change position.

Let’s look again at the operators in the infix expression. The first operator that appears from left to right is +. However, in the postfix expression, + is at the end since the next operator, ·, has precedence over addition. The order of the operators in the original expression is reversed in the resulting postfix expression.

As we process the expression, the operators have to be saved somewhere since their corresponding right operands are not seen yet. Also, the order of these saved operators may need to be reversed due to their precedence.

Because of this reversal of order, it makes sense to consider using a stack to keep the operators until they are needed! What about (A + B) · C? Recall that A B + C · is the postfix equivalent. Again, processing this infix expression from left to right, we see + first. In this case, when we see ·, + has already been placed in the result expression because it has precedence over · by virtue of the parentheses.

The conversion algorithm works by saving a left parenthesis to indicate the upcoming arrival of a high-precedence operator, which waits for the corresponding right parenthesis to determine its position. When the right parenthesis appears, the operator is popped from the stack.

1. Create an empty stack (op_stack) for operators and an empty list for output.
2. Convert the input infix string to a list using the string method split().

3. Scan the token list from left to right:
   • Append operands to the output list.
   • Push left parentheses onto op_stack.
   • For right parentheses, pop op_stack until the left parenthesis is removed, appending each operator to the output list.
   • Push operators (·, /, +, -) onto op_stack after removing any higher or equal precedence operators from the stack and appending them to the output list.

4. After processing the input expression, remove any remaining operators from op_stack and append them to the output list.

from pythonds3.basic import Stack

def infix_to_postfix(infix_expr):
    prec = {"*": 3, "/": 3, "+": 2, "-": 2, "(": 1}
    op_stack = Stack()
    postfix_list = []
    token_list = infix_expr.split()

    for token in token_list:
        if token.isalnum():
            postfix_list.append(token)
        elif token == '(':
            op_stack.push(token)
        elif token == ')':
            while (not op_stack.is_empty()) and op_stack.peek() != '(':
                postfix_list.append(op_stack.pop())
            op_stack.pop()  # Pop '('
        else:
            while (not op_stack.is_empty()) and (prec[op_stack.peek()] >= prec[token]):
                postfix_list.append(op_stack.pop())
            op_stack.push(token)

    while not op_stack.is_empty():
        postfix_list.append(op_stack.pop())

    return ' '.join(postfix_list)

print(infix_to_postfix("A * B + C * D"))
print(infix_to_postfix("( A + B ) * C - ( D - E ) * ( F + G )"))

A B * C D * +
A B + C * D E - F G + * -

3.9.3. Postfix Evaluation

We will now consider the evaluation of an expression that is already in postfix notation. In this case, a stack is again the data structure of choice. However, as you scan the postfix expression, it is the operands that must wait, not the operators as in the conversion algorithm above.

Another way to think about the solution is that whenever an operator is seen on the input, the two most recent operands will be used in the evaluation.

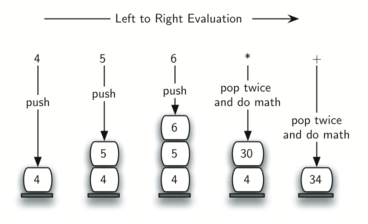
To see this in more detail, consider the postfix expression 4 5 6 · +. As you scan the expression from left to right, you first encounter the operands 4 and 5. At this point, you are still unsure what to do with them until you see the next symbol. Placing each on the stack ensures that they are available if an operator comes next.

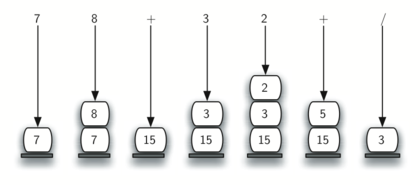
A slightly more complex example, 7 8 + 3 2 + /. First, the stack size grows, shrinks, and then grows again as the subexpressions are evaluated. Second, the division operation needs to be handled carefully. Recall that the operands in the postfix expression are in their original order since postfix changes only the placement of operators. When the operands for the division are popped from the stack, they are reversed. Since division is not a commutative operator, we must be sure that the order of the operands is not switched!

1. Create an empty stack called operand_stack.
2. Convert the string to a list by using the string method split().

3. Scan the token list from left to right.
   • If the token is an operand, convert it from a string to an integer and push the value onto the operand_stack.
   • If the token is an operator, ·, /, +, or -, it will need two operands. Pop the operand_stack twice. The first pop is the second operand and the second pop is the first operand. Perform the arithmetic operation. Push the result back on the operand_stack.
4. When the input expression has been completely processed, the result is on the stack. Pop the operand_stack and return the value.

To assist with the arithmetic, a helper function do_math is defined:

def do_math(op, op1, op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

from pythonds3.basic import Stack

def postfix_eval(postfix_expr):
    operand_stack = Stack()
    token_list = postfix_expr.split()

    for token in token_list:
        if token in "0123456789":
            operand_stack.push(int(token))
        else:
            operand2 = operand_stack.pop()
            operand1 = operand_stack.pop()
            result = do_math(token, operand1, operand2)
            operand_stack.push(result)
    return operand_stack.pop()

print(postfix_eval("7 8 + 3 2 + /"))

3.0

It is important to note that in both the postfix conversion and the postfix evaluation programs we assumed that there were no errors in the input expression.

Exercise: Modify the infix_to_postfix() function so that it can convert the following expression: 5 * 3 ^ (4 - 2). Run the function on the expression and paste the answer here:

from pythonds3.basic import Stack

def infix_to_postfix(infix_expr):
    prec = {"*": 3, "/": 3, "+": 2, "-": 2, "(": 1}
    op_stack = Stack()
    postfix_list = []
    token_list = infix_expr.split()

    for token in token_list:
        if token.isalnum():
            postfix_list.append(token)
        elif token == '(':
            op_stack.push(token)
        elif token == ')':
            while (not op_stack.is_empty()) and op_stack.peek() != '(':
                postfix_list.append(op_stack.pop())
            op_stack.pop()  # Pop '('
        else:
            while (not op_stack.is_empty()) and (prec[op_stack.peek()] >= prec[token]):
                postfix_list.append(op_stack.pop())
            op_stack.push(token)

    while not op_stack.is_empty():
        postfix_list.append(op_stack.pop())

    return ' '.join(postfix_list)

def do_math(op, op1, op2):
    if op == "*":
        return op1 * op2
    elif op == "/":
        return op1 / op2
    elif op == "+":
        return op1 + op2
    else:
        return op1 - op2

print(infix_to_postfix("5 * 3 ^ ( 4 - 2 )"))
print(postfix_eval(infix_to_postfix("5 * 3 ^ ( 4 - 2 )")))

3.10. Queues

A queue is an ordered collection of items where the addition of new items happens at one end, called the rear, and the removal of existing items occurs at the other end, commonly called the front. As an element enters the queue it starts at the rear and makes its way toward the front, waiting until that time when it is the next element to be removed. The item that has been in the collection the longest is at the front. This ordering principle is sometimes called FIFO, first in, first out.

The simplest example of a queue is that we wait in a line for a movie, we wait in the checkout line at a grocery store, and we wait in the cafeteria line.

Well-behaved lines, or queues, are very restrictive in that they have only one way in and only one way out. There is no jumping in the middle and no leaving before you have waited the necessary amount of time to get to the front.

Computer science also has common examples of queues. Figure shows a simple queue of Python data objects.

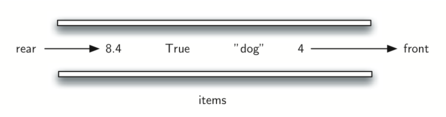
Operating systems use a number of different queues to control processes within a computer. The scheduling of what gets done next is typically based on a queuing algorithm that tries to execute programs as quickly as possible and serve as many users as it can.

3.11 The Queue Abstract Data Type

The queue operations are given below:

• Queue() creates a new queue that is empty. It needs no parameters and returns an empty queue.

• enqueue(item) adds a new item to the rear of the queue. It needs the item and returns nothing.
• dequeue() removes the front item from the queue. It needs no parameters and returns the item. The queue is modified.

• is_empty() tests to see whether the queue is empty. It needs no parameters and returns a boolean value.
• size() returns the number of items in the queue. It needs no parameters and returns an integer.

Table below shows the results of a sequence of queue operations. The queue contents are shown such that the front is on the right.

Queue Operation	Queue Contents	Return Value
q.is_empty()	[]	True
q.enqueue(4)	[4]
q.enqueue("dog")	['dog', 4]
q.enqueue(True)	[True, 'dog', 4]
q.size()	[True, 'dog', 4]	3
q.is_empty()	[True, 'dog', 4]	False
q.enqueue(8.4)	[8.4, True, 'dog', 4]
q.dequeue()	[8.4, True, 'dog']	4
q.dequeue()	[8.4, True]	'dog'
q.size()	[8.4, True]	2

3.12 Implementing a Queue in Python

The implementation assumes that the rear is at position 0 in the list. This allows us to use the insert() function on lists to add new elements to the rear of the queue. The pop() operation can be used to remove the front element. Recall that this also means that enqueue will be $O(n)$ and dequeue will be $O(1)$.

class Queue:
    def __init__(self):
        """Create new queue"""
        self._items = []

    def is_empty(self):
        """Check if the queue is empty"""
        return not bool(self._items)

    def enqueue(self, item):
        """Add an item to the queue"""
        self._items.insert(0, item)

    def dequeue(self):
        """Remove an item from the queue"""
        return self._items.pop()

    def size(self):
        """Get the number of items in the queue"""
        return len(self._items)

q = Queue()
q.enqueue(4)
q.enqueue("dog")
q.enqueue(True)
print(q.size())
print(q.is_empty())

3
False

3.13. Queue Simulation: Hot Potato

To begin, let’s consider the children’s game hot potato. In this game, children line up in a circle and pass an item from neighbor to neighbor as fast as they can. At a certain point in the game, the action is stopped and the child who has the item (the potato) is removed from the circle. Play continues until only one child is left.

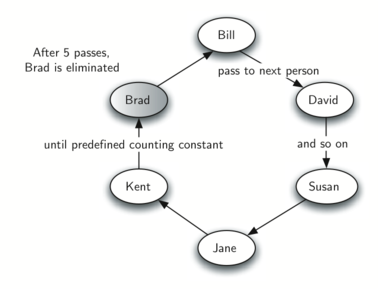
We will implement a general simulation of Hot Potato. Our program will input a list of names and a constant, call it "num," to be used for counting. It will return the name of the last person remaining after repetitive counting by num.

To simulate the circle, we will use a queue. Assume that the child holding the potato will be at the front of the queue. Upon passing the potato, the simulation will simply dequeue and then immediately enqueue that child, putting them at the end of the line.

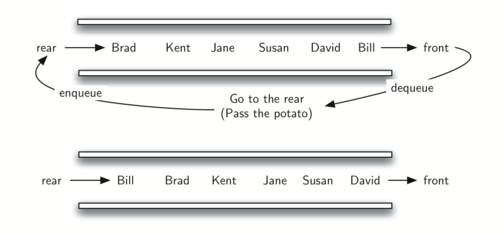
After num dequeue/enqueue operations, the child at the front will be removed permanently and another cycle will begin. This process will continue until only one name remains (the size of the queue is 1)!

from pythonds3.basic import Queue

def hot_potato(name_list, num):
    sim_queue = Queue()
    for name in name_list:
        sim_queue.enqueue(name)

    while sim_queue.size() > 1:
        for i in range(num):
            sim_queue.enqueue(sim_queue.dequeue())

        sim_queue.dequeue()

    return sim_queue.dequeue()

print(hot_potato(["Bill", "David", "Susan", "Jane", "Kent", "Brad"], 7))

Susan

Notice that the list is loaded into the queue such that the first name on the list will be at the front of the queue. 'Bill' in this case is the first item in the list and therefore moves to the front of the queue.

Exercise: Implement the queue ADT, using a list such that the rear of the queue is at the end of the list.

## Your code here

3.15 Deques

A deque, also known as a double-ended queue, is an ordered collection of items similar to the queue. It has two ends, a front and a rear. What makes a deque different is the unrestrictive nature of adding and removing items.

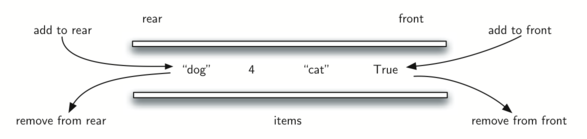
New items can be added at either the front or the rear. Likewise, existing items can be removed from either end. In a sense, this hybrid linear structure provides all the capabilities of stacks and queues in a single data structure.

3.16 The Deque Abstract Data Type

The deque operations are given below:

• Deque() creates a new deque that is empty. It needs no parameters and returns an empty deque.

• add_front(item) adds a new item to the front of the deque. It needs the item and returns nothing.
• add_rear(item) adds a new item to the rear of the deque. It needs the item and returns nothing.
• remove_front() removes the front item from the deque. It needs no parameters and returns the item. The deque is modified.
• remove_rear() removes the rear item from the deque. It needs no parameters and returns the item. The deque is modified.

• is_empty() tests to see whether the deque is empty. It needs no parameters and returns a boolean value.
• size() returns the number of items in the deque. It needs no parameters and returns an integer.

The contents in front are listed on the right. It is very important to keep track of the front and the rear as you move items in and out of the collection as things can get a bit confusing.

Deque Operation	Deque Contents	Return Value
d.is_empty()	[]	True
d.add_rear(4)	[4]
d.add_rear("dog")	['dog', 4]
d.add_front("cat")	['dog', 4, 'cat']
d.add_front(True)	['dog', 4, 'cat', True]
d.size()	['dog', 4, 'cat', True]	4
d.is_empty()	['dog', 4, 'cat', True]	False
d.add_rear(8.4)	[8.4, 'dog', 4, 'cat', True]
d.remove_rear()	['dog', 4, 'cat', True]	8.4
d.remove_front()	['dog', 4, 'cat']	True

3.17. Implementing a Deque in Python

Our implementation will assume that the rear of the deque is at position 0 in the list.

class Deque:
    """Deque implementation as a list"""
    def __init__(self):
        """Create new deque"""
        self._items = []
    def is_empty(self):
        """Check if the deque is empty"""
        return not bool(self._items)
    def add_front(self, item):
        """Add an item to the front of the deque"""
        self._items.append(item)
    def add_rear(self, item):
        """Add an item to the rear of the deque"""
        self._items.insert(0, item)
    def remove_front(self):
        """Remove an item from the front of the deque"""
        return self._items.pop()
    def remove_rear(self):
        """Remove an item from the rear of the deque"""
        return self._items.pop(0)
    def size(self):
        """Get the number of items in the deque"""
        return len(self._items)

You can see many similarities to Python code already described for stacks and queues. You are also likely to observe that in this implementation adding and removing items from the front is $O(1)$ whereas adding and removing from the rear is $O(n)$. This is to be expected given the common operations that appear for adding and removing items. Again, the important thing is to be certain that we know where the front and rear are assigned in the implementation.

3.18 Palindrome Checker

A palindrome is a string that reads the same forward and backward, for example, radar, toot, and madam. We would like to construct an algorithm to input a string of characters and check whether it is a palindrome.

The solution to this problem will use a deque to store the characters of the string. We will process the string from left to right and add each character to the rear of the deque. At this point, the deque will be acting very much like an ordinary queue.

However, we can now make use of the dual functionality of the deque. The front of the deque will hold the first character of the string and the rear of the deque will hold the last character.

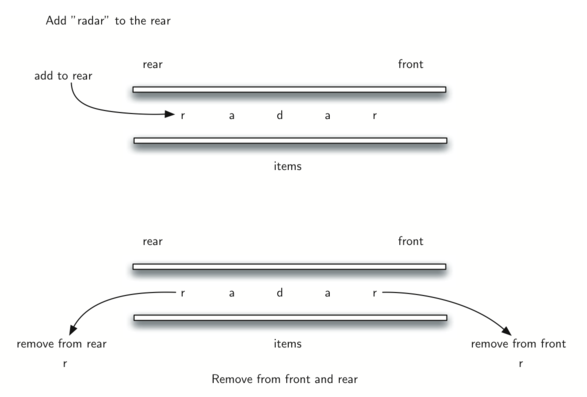
Since we can remove both of the front and rear characters directly, we can compare them and continue only if they match. If we can keep matching first and the last items, we will eventually either run out of characters or be left with a deque of size 1 depending on whether the length of the original string was even or odd. In either case, the string must be a palindrome.

from pythonds3.basic import Deque

def pal_checker(a_string):
    char_deque = Deque()

    for ch in a_string:
        char_deque.add_rear(ch)

    while char_deque.size() > 1:
        first = char_deque.remove_front()
        last = char_deque.remove_rear()
        if first != last:
            return False

    return True

print(pal_checker("lsdkjfskf"))
print(pal_checker("radar"))

References

1. Textbook CH3